Cientistas usam os mesmos termos do gráfico da função seno para descrever as ondas marítimas. O período de uma onda marítima é o intervalo de tempo entre uma crista e a seguinte e a distância entre elas é o comprimento da onda. A figura descreve, no plano cartesiano, uma onda marítima, em que o eixo vertical representa a altura das cristas da onda, e o eixo horizontal representa a distância percorrida pela onda.
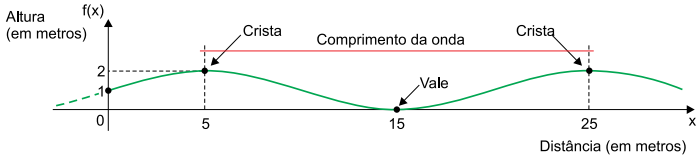
a) Sendo f: |R → |R, tal que f(x) = m + sen (n ⋅ x), a função referente ao gráfico apresentado, determine m e n.
b) Uma onda marítima foi modelada por meio da função g: |R → |R, tal que . Determine a altura de suas cristas e o comprimento da onda.
a) Do gráfico, tem-se f(0) = 1. Logo, m + sen(n·0) = 1 e, portanto, m = 1.
Além disso, o período da função trigonométrica vale 25 – 5 = 20. Portanto, e, assim,
. Como f(5) = 2, então note que
(pois, caso contrário, f(5) ≠ 2).
b) Entendendo a altura como todos os possíveis valores das imagens da função, tem-se:
Considerando a altura da crista como o valor máximo de g(x), temos que sua altura é de 4m.
O comprimento da onda é dado pelo período da função trigonométrica e vale .