Um fio retilíneo de arame de comprimento de 9,25 cm será dobrado, em ângulos retos, em dois pontos, Q e R. Tais dobras produzem três segmentos de retas de medidas: PQ = 4 cm, QR = 3 cm e . Já com as dobras, o fio de arame deverá encaixar-se perfeitamente no quadrado TSUP, de diagonal , como mostram as figuras.
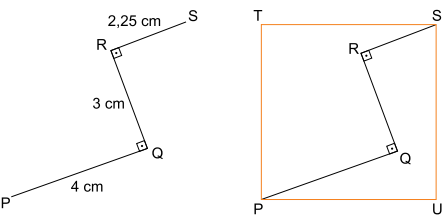
a) Calcule a medida do segmento , em centímetros, e a medida do segmento
, em milímetros.
b) Calcule a área do quadrado TSUP, em cm2.
a) Aplicando o teorema de Pitágoras nos triângulos retângulos PQR e QRS, respectivamente, tem-se PR2 = 42 + 32 e QS2 = 32 + 2,252, ou seja, PR = 5 cm e QS = 3,75 cm.
b) Observe a figura:
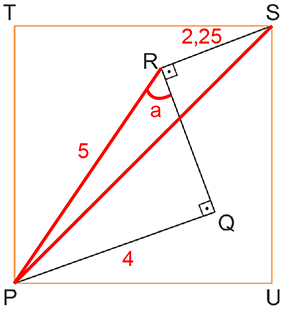
Primeiramente, note que cos(α + 90º) = –sen α. Além disso, no triângulo retângulo, tem-se .
Em seguida, aplicando o teorema dos cossenos no triângulo PRS, vem:
Sendo x a medida do lado do quadrado, então e, assim:
Portanto, a área do quadrado vale .