Em um dia de mar agitado, um banhista flutua na água e é atingido por uma onda senoidal de amplitude constante. Essa onda propaga-se para a direita com velocidade constante, fazendo com que o banhista oscile em movimento harmônico simples na direção vertical. As figuras 1 e 2 mostram o banhista e a configuração da água do mar nos instantes t = 0 e t = 3 s, respectivamente, antes de o banhista efetuar uma oscilação completa.
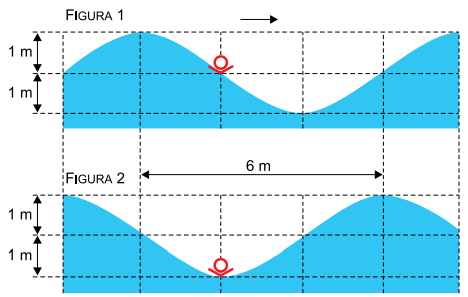
a) Calcule a velocidade de propagação da onda, em m/s, e a frequência de oscilação do banhista, em Hz.
b) Calcule o módulo da velocidade escalar média, em m/s, do banhista entre t = 0 e t = 3 s. Adotando π = 3, calcule o módulo da máxima velocidade instantânea, em m/s, do banhista, em seu movimento oscilatório.
a) A velocidade da onda pode ser determinada pela velocidade de deslocamento da crista em destaque no esquema a seguir.
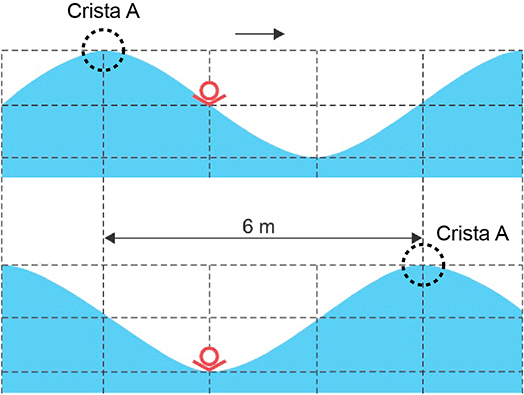
Uma vez que a velocidade é constante:
Note que 6 m corresponde a do comprimento de onda. Algebricamente:
A partir da equação da ondulatória v = λ·f, temos:
2 = 8·f
Assim, a frequência de oscilação do banhista (fb), que corresponde à frequência da onda, vale:
fb = 0,25 Hz
b) O módulo da velocidade escalar média do banhista (vmB) pode ser determinado por:
Note que, no intervalo de tempo considerado (entre 0 e 3s), o módulo do deslocamento escalar do banhista é 1m.
Assim:
A velocidade máxima do banhista que oscila em MHS é dada por:
Em que A é a amplitude de oscilação e vale 1 m.
Fazendo as devidas substituições numéricas:
Portanto: