Uma pessoa de 70 kg está em repouso na extremidade de uma tábua rígida de massa desprezível, mantida em equilíbrio na direção horizontal e presa na borda de um tanque contendo água. Dessa posição, a pessoa consegue ver a imagem de um peixe parado dentro do tanque. Na figura, está representado um raio de luz proveniente do peixe, que atinge o olho dessa pessoa.
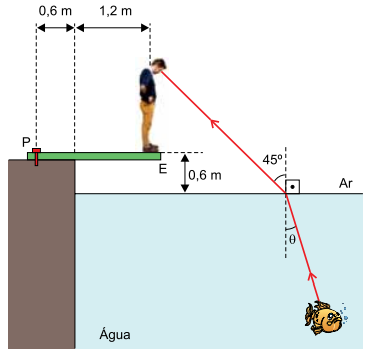
a) Sabendo que a tábua é presa à borda do tanque por um único pino P, indicado na figura, e adotando g = 10 m/s2, calcule, em newtons, a intensidade da força aplicada pela pessoa sobre a tábua e a intensidade da força aplicada pelo pino sobre a tábua.
b) Considerando o índice de refração relativo da água em relação ao ar igual a , obtenha o ângulo θ, indicado na figura. Em seguida, sabendo que os olhos dessa pessoa estão a 1,5 m de altura da tábua, calcule a distância, em metros, entre os olhos da pessoa e a imagem da extremidade E da tábua, formada pela superfície da água do tanque, considerando essa superfície como um espelho plano.
a) O esquema a seguir indica as forças aplicadas sobre a tábua.
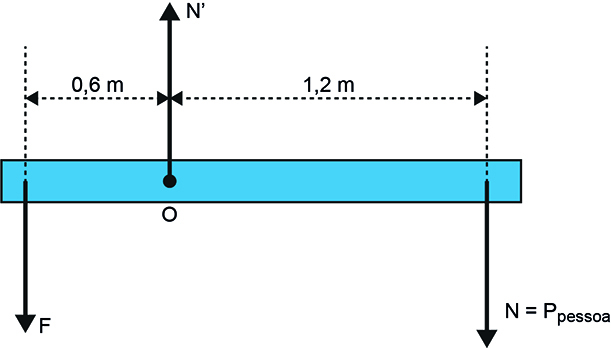
Em que:
força exercida pelo pino;
normal aplicada pelo apoio;
normal aplicada pela pessoa.
Assim, a intensidade da força aplicada pela pessoa sobre a tábua é:
Por estar em equilíbrio, podemos afirmar que a soma dos momentos das forças aplicadas à tábua em relação ao ponto O é nulo. Adotando o sentido horário como positivo:
b) Aplicando a lei de Snell à situação apresentada, segue:
Adotando nar = 1 e fazendo as devidas substituições numéricas:
Portanto:
O esquema a seguir mostra a imagem da extremidade E, formada pela superfície de separação do dioptro.
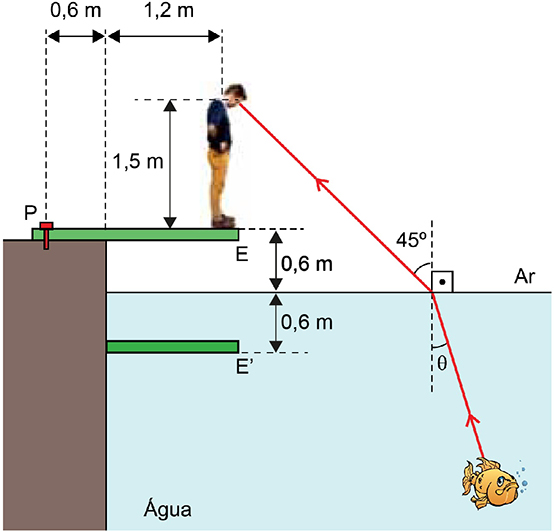
Assim, a distância entre os olhos da pessoa e a imagem da extremidade E da tábua, formada pela superfície da água do tanque, vale 2,7 m.