Um gás monoatômico ideal está confinado em um recipiente e sofre a transformação cíclica ABCA indicada no diagrama P × V, em que BC é uma transformação isotérmica.
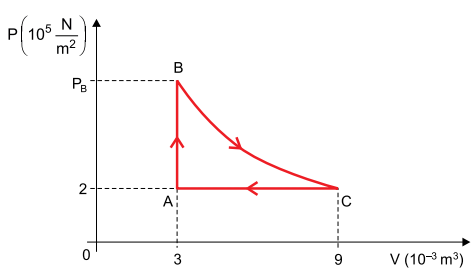
Sabendo que a temperatura do gás no estado A é 300 K e adotando, para a constante universal dos gases ideais, o valor 8 J/(mol ⋅ K), calcule:
a) o trabalho, em joules, realizado pelas forças que o gás exerce sobre as paredes do recipiente na transformação AB e na transformação CA.
b) o número de mols de gás existente dentro do recipiente e a pressão, em N/m2, exercida pelo gás no estado B.
a) Como apresentado no diagrama pressão x volume, tem-se:
- Transformação AB:
Por se tratar de uma transformação isométrica, o trabalho é nulo;
- Transformação CA:
Sendo uma transformação isobárica, pode-se determinar o trabalho das forças exercidas pelo gás por meio da expressão a seguir:
Finalmente, tem-se:
b) Inicialmente, pode-se determinar a pressão no estado B por meio da equação geral dos gases, sendo que a transformação BC é isotérmica:
Para se determinar o número de mols no recipiente, pode-se utilizar a equação de Clapeyron: