Uma bola de 0,4 kg é chutada com velocidade inicial V0 = 20 m/s do ponto A, na encosta de um morro, e, depois de descrever um arco de parábola no ar, toca novamente a encosta desse morro no ponto C, que está verticalmente 15 m abaixo do ponto A. No percurso do ponto A ao ponto C, a bola atinge o ponto B, ponto mais alto de sua trajetória, conforme mostra a figura.
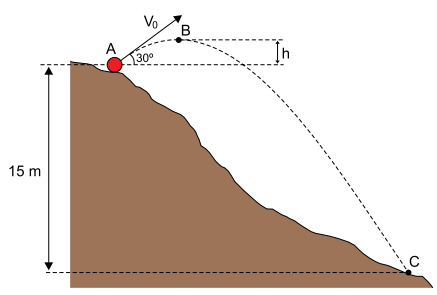
Sabendo que, no momento do chute, a velocidade inicial da bola está inclinada de 30º com a horizontal, desprezando a resistência do ar e adotando g = 10 m/s2, calcule:
a) a energia cinética da bola, em joules, imediatamente após o chute e imediatamente antes de tocar o solo, no ponto C.
b) a distância vertical h, em metros, entre o ponto A e o ponto B. Em seguida, calcule o tempo, em segundos, para que a bola vá do ponto A ao ponto C.
a)
- Determinação da energia cinética da bola imediatamente após o chute, no ponto A.
A energia cinética pode ser calculada pela seguinte expressão:
Sendo m = 0,4 kg e VA = V0 = 20 m/s:
- Determinação da energia cinética da bola imediatamente antes de tocar o solo, no ponto C.
Como o sistema é conservativo:
Sendo e
, temos:
b) Para a situação descrita pelo enunciado, temos:
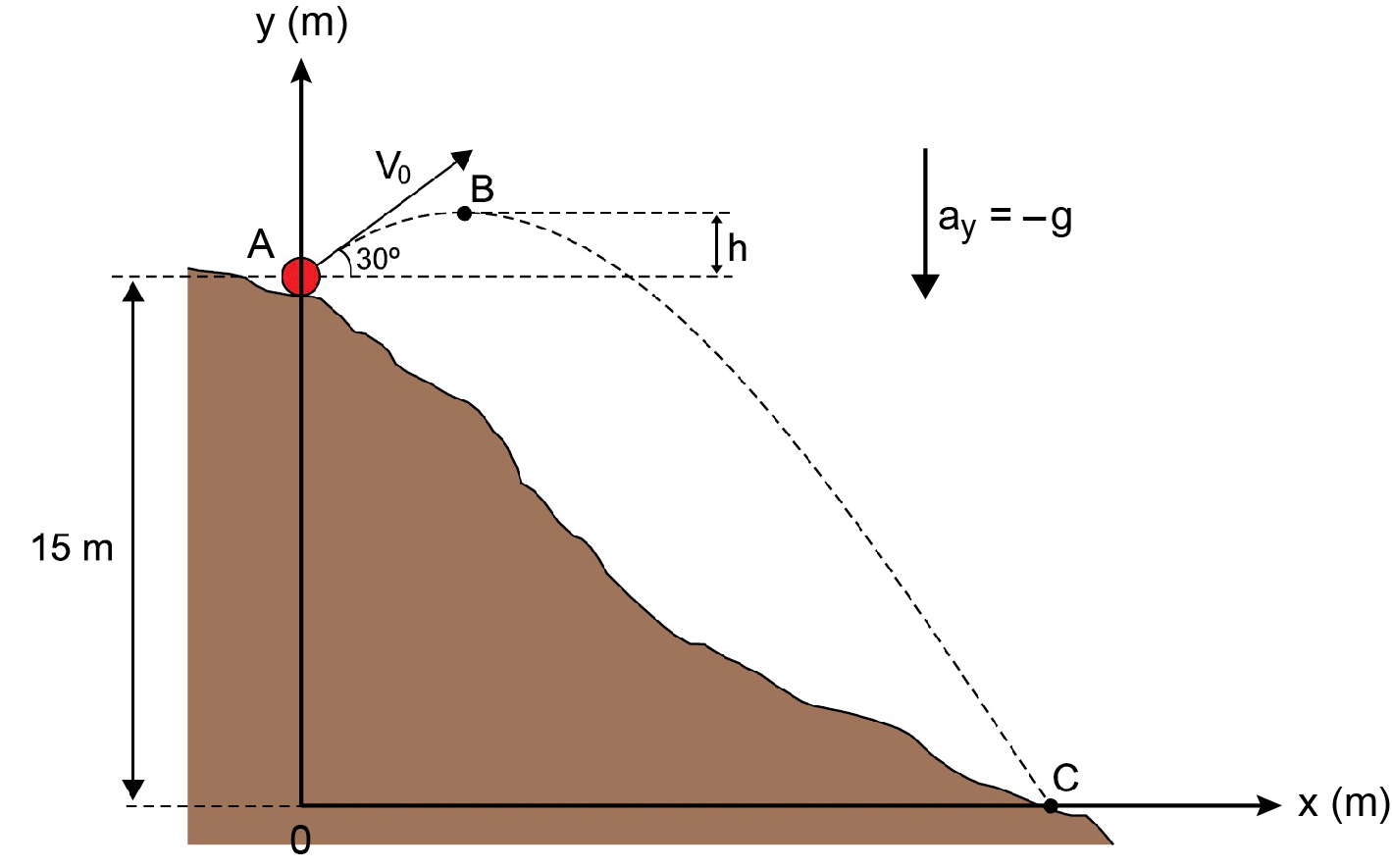
- Determinação da distância vertical entre os pontos A e B
A componente vertical da velocidade pode ser obtida da seguinte maneira:
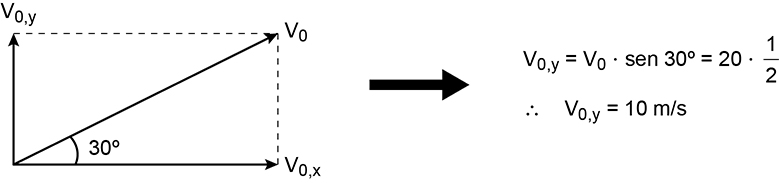
Logo, aplicando-se a equação de Torricelli para o movimento vertical:
Como, no ponto mais alto do lançamento oblíquo, a componente vertical da velocidade é nula:
- Determinação do intervalo de tempo para a bola ir de A até C
Aplicando-se a equação dos espaços para o movimento vertical:
Sendo y = 0 e y0 = 15 m:
Resolvendo-se a equação do 2º grau em t e descartando-se a resposta negativa, obtém-se t = 3 s.