Em artigo publicado em 2022, uma física e um físico brasileiros propuseram uma interessante analogia entre congestionamentos de carros e a física de buracos negros (Luanna K. de Souza, George E. A. Matsas, “Black-hole analog in vehicular traffic”, American J. of Phys. 90, 692 (2022)).
Considere uma fila de 9 carros inicialmente em posições x0, x1, x2,….,x8 separados um do outro por uma distância D e se movendo com velocidade constante v na direção negativa de um eixo x.
No instante inicial, o carro 0 freia, acionando sua luz de freio. Após um tempo de reação T1, o carro 1 freia, acionando agora a sua luz de freio. O carro 2, por sua vez, freia e aciona sua luz de freio um tempo T2 após o carro 1 acionar a sua luz de freio e assim sucessivamente.
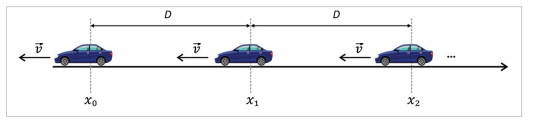
Para este problema, considere que no instante da primeira frenagem (instante inicial): (i) o carro 0 esteja localizado na origem (x0 = 0); (ii) a distância entre os carros seja de D = 20 m; e (iii) todos os carros tenham a mesma velocidade escalar || = vini.
a) Dada a velocidade vini = 72 km/h, calcule o tempo de reação máximo Tmáx para que não ocorram colisões entre quaisquer dois carros.
Texto para os itens (b) e (c):
Em geral, os tempos de reação dos motoristas não são iguais. Por exemplo, se os primeiros carros estiverem envoltos em neblina ou fumaça, os tempos de reação serão maiores para os primeiros carros da fila e menores para os últimos carros da fila. Considere a tabela a seguir, que mostra os tempos de reação T1, T2,…,T8 (em segundos) retratando uma situação como essa.

Se o tempo de reação de um dado carro for maior que Tmáx, este carro inevitavelmente irá colidir com o carro da frente. Em uma analogia proposta pelos autores do artigo, este carro entra no “horizonte de eventos” de um “buraco negro veicular”.
b) Suponha agora uma outra velocidade vini tal que Tmáx = 0,89 s. Utilizando os dados da tabela, determine, em metros, a posição do “horizonte de eventos”, ou seja, a posição xH tal que todos os carros com posição inicial xj ≤ xH inevitavelmente colidirão com o carro da frente.
c) Calcule o intervalo de velocidades vini compatível com xH = 60 m.
Note e adote:
Assuma que a distância entre os carros D seja muito maior que o comprimento dos carros. Considere que, dada a velocidade vini, após o acionamento dos freios, todos os carros que não colidem percorrem uma mesma distância até atingirem o repouso. Tempo de reação: O intervalo de tempo que o motorista demora para acionar o freio após ver o sinal emitido pelo carro da frente. Horizonte de eventos de um buraco negro: Superfície teórica em torno de seu centro a partir da qual nenhum outro evento pode fazer com que um objeto ou radiação escape de, eventualmente, ser sugado em direção ao centro do buraco negro. No caso do “buraco negro veicular” é o ponto a partir do qual um carro inevitavelmente irá colidir com o carro da frente e não pode escapar de uma colisão em seu futuro do mesmo modo que nada (nem a luz) escapa de um buraco negro real.
a) As distâncias percorridas pelos carros durante as desacelerações são iguais. Dessa forma, o máximo do tempo de reação Tmáx corresponde ao intervalo de tempo em que o carro anterior se desloca em uma distância D a uma velocidade constante igual a 20 m/s. Dessa forma, como a velocidade do carro anterior é constante, sua velocidade escalar instantânea é igual à sua velocidade escalar média:
b) A partir da tabela fornecida no enunciado, vemos que os carros de 1 a 5 colidirão, enquanto os carros de 6 a 8, não.

Dessa forma, observando-se que os valores possíveis para a posição do horizonte de eventos correspondem às posições dos carros, seu valor corresponde à posição inicial do carro 5. A tabela a seguir ilustra as posições iniciais dos carros:
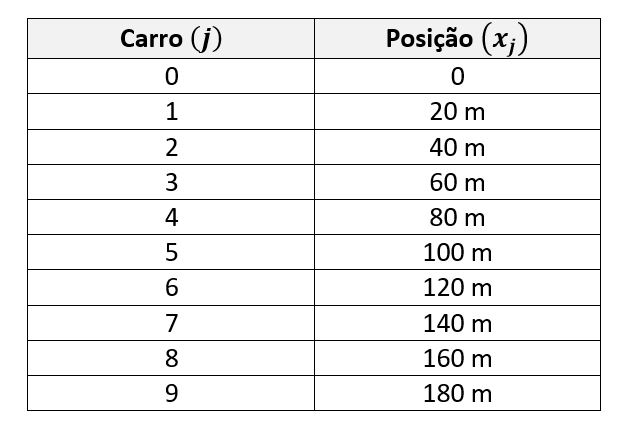
Dessa forma, xH = x5.
c) A posição do horizonte de eventos xH = 60 m, corresponde à posição inicial do carro 3. Dessa forma,
- o carro 3 colide. Assim, a menor velocidade em módulo corresponde àquela em que o carro 3 desloca 20 m (em módulo), durante um intervalo de tempo igual a T3 = 1,6 s. Como sua velocidade é constante:
- o carro 4 não deve colidir. Assim, a velocidade em módulo deve ser menor que àquela com a qual o carro 4 colidiria. Como o tempo de reação desse carro é igual à T4 = 1 s, essa velocidade é igual a 20 m/s (item a).
Portanto, o intervalo de velocidade vini compatível é .