O efeito Doppler é caracterizado pela detecção de uma frequência diferente daquela emitida pela fonte, devido ao movimento relativo entre fonte e observador. Ele possui diversas aplicações, seja na medicina, astronomia ou ainda em sonares de velocidade, nos quais a velocidade de um objeto é medida comparando-se a frequência sonora emitida com aquela que é detectada.

Considere um sonar de velocidade que envia ondas sonoras de 0,10 MHz em direção a um veículo que se aproxima com velocidade desconhecida.

a) Calcule o comprimento de onda emitido pelo sonar.

b) Suponha que exista um detector de ondas sonoras no carro. Calcule a frequência detectada por este detector considerando que o carro se aproxima do sonar com velocidade de 30 m/s.

c) Encontre a velocidade do veículo sabendo que o sonar detecta uma frequência de 0,15 MHz refletida de volta, do carro para o sonar.

Note e adote:
Considere a velocidade do som como 300 m/s.
No efeito Doppler, a frequência fd detectada pelo observador e a frequência fe emitida pela fonte se relacionam de acordo com a expressão: começar estilo tamanho matemático 14px numerador f com d subscrito sobre denominador v com s subscrito mais ou menos v com d subscrito fim da fração igual a numerador f com e subscrito sobre denominador v com s subscrito mais ou menos v com e subscrito fim da fração fim do estilo, onde vs é a velocidade do som, vd é a velocidade do observador e ve é a velocidade da fonte de emissão. Os sinais "+" e "−" são escolhidos de acordo com o movimento relativo entre fonte e observador.

a) Usando a equação fundamental da ondulatória (v = λ·f), em que v = 300 m/s e f = 0,1·106 Hz, temos:

começar estilo tamanho matemático 14px 300 igual a reto lambda vezes 0 vírgula 1 vezes 10 à potência de 6 fim do estilo

começar estilo tamanho matemático 14px então espaço reto lambda igual a 3 vezes 10 à potência de menos 3 fim do exponencial espaço reto m igual a 3 espaço mm fim do estilo

b) O esquema a seguir, representa a situação, com orientação da trajetória do observador (carro) à fonte.

Usando a equação fornecida para o efeito Doppler:

começar estilo tamanho matemático 14px numerador reto f com reto d subscrito sobre denominador 300 mais 30 fim da fração igual a numerador 1 vezes 10 à potência de 5 sobre denominador 300 mais 0 fim da fração fim do estilo

Segue:

começar estilo tamanho matemático 14px reto f com reto d subscrito igual a 1 vírgula 1 vezes 10 à potência de 5 espaço Hz igual a 0 vírgula 11 espaço MHz fim do estilo

c) Usando o mesmo esquema anterior para essa nova situação, temos:

Vamos, inicialmente, determinar a frequência detectada pelo carro.

começar estilo tamanho matemático 14px numerador reto f com reto d subscrito sobre denominador 300 mais reto v fim da fração igual a numerador 1 vezes 10 à potência de 5 sobre denominador 300 mais 0 fim da fração seta dupla para a direita fim do estilocomeçar estilo tamanho matemático 14px reto f com reto d subscrito igual a numerador 300 mais reto v sobre denominador 300 fim da fração vezes 1 vezes 10 à potência de 5 fim do estilo

A seguir, podemos imaginar que o carro passa a ser a fonte emissora de ondas (a onda detectada por ele) e o observador passa a ser o aparelho de sonar. O novo esquema, com a nova orientação (do observador para a fonte) será:

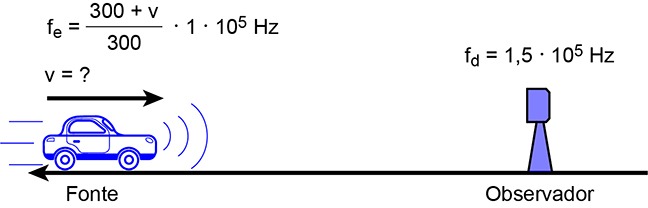
Usando a equação fornecida:

começar estilo tamanho matemático 14px numerador 1 vírgula 5 vezes 10 à potência de 5 sobre denominador 300 mais 0 fim da fração igual a numerador começar estilo mostrar numerador 300 mais reto v sobre denominador 300 fim da fração fim do estilo vezes 1 vezes 10 à potência de 5 sobre denominador 300 menos reto v fim da fração seta dupla para a direita fim do estilocomeçar estilo tamanho matemático 14px reto f com reto d subscrito igual a numerador 300 mais reto v sobre denominador 300 fim da fração vezes 1 vezes 10 à potência de 5 espaço Hz fim do estilo

Segue que a velocidade (v) do veículo é v = 60 m/s.