Um circuito é formado por dois resistores em paralelo imersos no vácuo, separados por uma distância d ligados a uma bateria de força eletromotriz V. Cada resistor é formado por um fio muito longo, de mesmo comprimento e área de seção transversal, mas com resistividades elétricas ρ1 e ρ2 diferentes entre si, conforme ilustrado na figura.
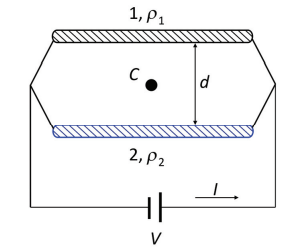
a) Sendo P1 e P2 as potências dissipadas nos resistores 1 e 2, respectivamente, calcule a razão P1/P2. Expresse sua resposta em termos de ρ1 e ρ2.
b) Considerando que a corrente total no circuito seja I, obtenha, em função de I, ρ1 e ρ2, o valor das correntes I1 e I2 que atravessam os resistores 1 e 2, respectivamente.
c) Obtenha a expressão para o módulo do campo magnético no ponto C, mostrado na figura, equidistante dos dois resistores, considerando I1 = I2/4. Expresse sua resposta somente em termos de d, μ0 (constante de permeabilidade magnética do vácuo) e da corrente total I.
Note e adote:
A resistência elétrica é diretamente proporcional ao comprimento, à resistividade e inversamente proporcional à área da seção transversal. O módulo do campo magnético produzido por um fio muito longo transportando uma corrente I a uma distância r é dado por μ0I/2πr, onde μ0 é a constante de permeabilidade do vácuo.
a) A razão entre as potências dissipadas pode assim ser obtida:
Como, de acordo com a figura dada, os dois resistores estão em paralelo, a diferença de potencial (U) entre seus terminais é a mesma (U1 = U2):
Utilizando a segunda Lei de Ohm:
De acordo com enunciado, o comprimento e as áreas transversais dos resistores (filiformes) 1 e 2 são iguais.
Portanto,
b) Como U1 = U2, temos que:
Utilizando a segunda Lei de Ohm:
Assim:
(1)
Como os resistores 1 e 2 estão em paralelo: (2)
Assim, substituindo (1) em (2), temos que:
(3)
Substituindo (3) em (1), temos que:
c) De acordo com o enunciado, e
. Assim, as correntes I1 e I2 em função da corrente total I são dadas por:
e
O esquema a seguir representa as correntes elétricas nos fios 1 e 2 e os campos magnéticos por elas produzidos:
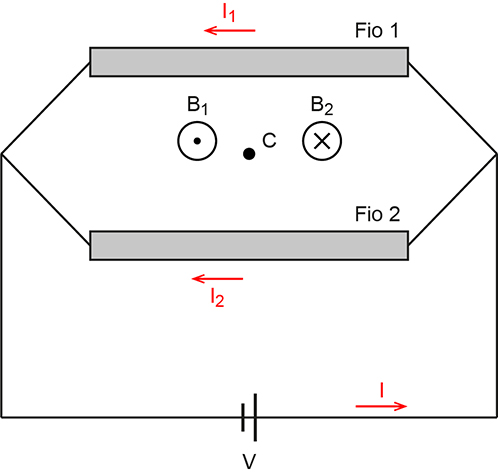
Como seus sentidos são opostos: