O telescópio espacial James Webb lançado em 2021 é, em muitos sentidos, um aprimoramento do antigo telescópico Hubble. Uma das diferenças mais notáveis está nas dimensões e nas propriedades ópticas dos espelhos principais destes dois telescópios. Por exemplo: enquanto o espelho principal do Hubble tem uma distância focal de aproximadamente 58 m, a distância focal do espelho principal do James Webb é de aproximadamente o dobro (131 metros). Tratando de maneira aproximada o funcionamento destes telescópios, consideraremos aqui a reflexão por somente um espelho esférico.
Suponha um sistema binário de estrelas separadas por uma distância H, e localizado a uma distância D do espelho do telescópio que as observa, conforme mostra a figura. A distância entre o foco do espelho (ponto F) e o vértice do espelho (ponto V) é a chamada distância focal do espelho (df).
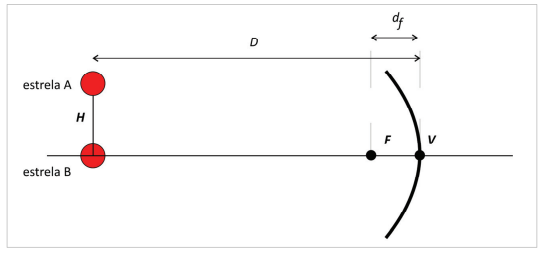
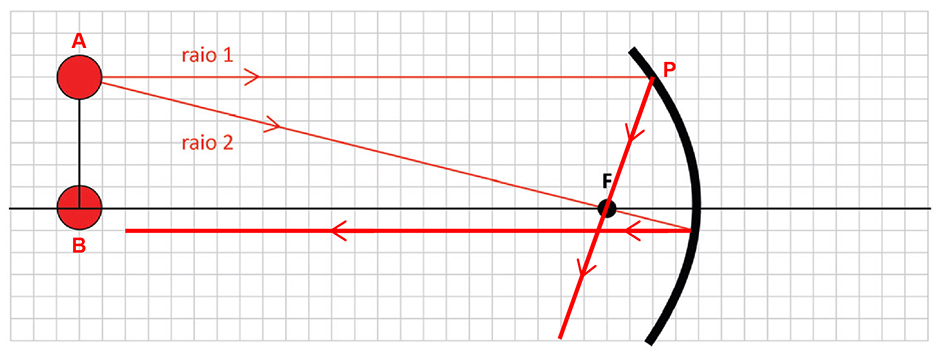
a) Dois raios luminosos (“raio 1” e “ raio 2”) partindo da estrela A atingem o espelho. O “raio 1” é paralelo ao eixo do espelho, enquanto o “raio 2” passa pelo ponto F. Na figura da folha de respostas, trace os raios refletidos pelo espelho.
b) Considere que o sistema está sendo observado pelo telescópio Hubble, para o qual df = d. Calcule a razão onde HI é a distância entre as imagens das estrelas formadas pelo espelho. Essa razão é também chamada de “aumento” do espelho, embora esta razão possa ser menor do que 1. Expresse sua resposta em termos de D e d.
c) Considere agora que o sistema esteja sendo observado pelo telescópio James Webb, para o qual df = 2d. Calcule a razão entre os aumentos dos dois espelhos. Expresse sua resposta em termos de D e d.
Note e adote:
As estrelas podem ser consideradas fontes luminosas pontuais.
Para espelhos esféricos, o inverso da distância focal é igual à soma do inverso da distância do objeto com o inverso da distância em que a imagem se forma (todas em relação ao centro do espelho).
a) De acordo com as propriedades relacionadas aos raios principais (ou raios notáveis) em espelhos esféricos, pode-se traçar as trajetórias dos raios indicados (1 e 2) como descritas e representadas a seguir:
- Raio 1: Como o raio de luz apresentado incide em uma direção paralela ao eixo principal do espelho, ele reflete na direção que contém o ponto de incidência (P) e o foco principal;
- Raio 2: Como esse raio de luz incide em uma direção formada pela extremidade do ponto A e o foco principal do espelho (F), ele reflete na direção paralela ao eixo principal do espelho.
b) Note que os valores H1 e H se referem a distâncias, logo, são elementos exclusivamente positivos. Assim sendo, a razão corresponde a
.
Assim, lembrando que , segue que
, em que f = d e p = D.
c) Considerando a expressão do aumento linear transversal para os dois telescópios considerados, tem-se:
- James Webb (AJW):
- Hubble (AH):
Desse modo, pode-se determinar a razão entre o aumento dos dois espelhos: