Considere as circunferências C, C1, C2, C3,…,Cn, … e a reta s satisfazendo as seguintes propriedades:

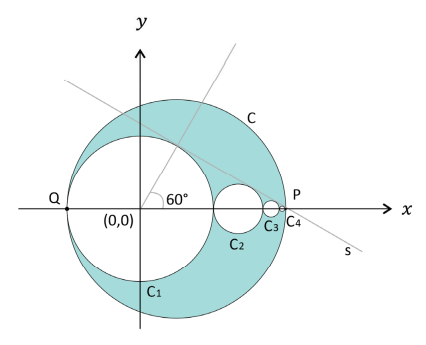
• A circunferência C1 tem centro (0,0) e raio r = 4. Os centros das demais circunferências pertencem ao eixo Ox.

• A circunferência C2 é tangente a C1 e a C3, a circunferência C3 é tangente a C2 e a C4, e assim por diante.

• A reta s é tangente a cada circunferência Cn para n ≥ 1.

• O segmento que liga o centro de C1 ao ponto em que s tangencia C1 forma um ângulo de 60° com o eixo Ox.

• A circunferência C é tangente a C1 no ponto Q = (−4,0) e passa pelo ponto P = (x0, 0).

Com base nessas informações,

a) determine o raio da circunferência C.

b) dado n ≥ 1, determine a razão entre os raios das circunferências consecutivas Cn+1 e Cn.

c) determine a área da região sombreada na figura.

a) Sendo R a medida do raio da circunferência C, podemos esboçar a seguinte figura:

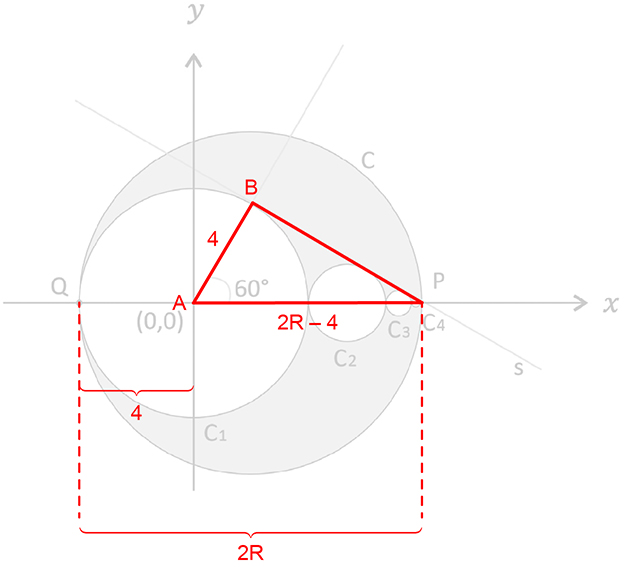
 Como o triângulo ABP é retângulo em B, temos:

começar estilo tamanho matemático 14px atributos de tabela alinhamento de coluna right center left espaçamento de coluna 0px fim dos atributos linha com célula com cos espaço 60 º espaço fim da célula igual a célula com espaço numerador 4 sobre denominador 2 reto R espaço menos espaço 4 fim da fração espaço espaço espaço espaço então fim da célula linha com célula com 1 meio espaço espaço fim da célula igual a célula com espaço numerador 4 sobre denominador 2 reto R espaço menos espaço 4 fim da fração espaço espaço espaço espaço então fim da célula linha com célula com reto R espaço fim da célula igual a célula com espaço 6 fim da célula fim da tabela fim do estilo

b) Pela figura, temos que a soma das medidas dos diâmetros das circunferências C1, C2, … é igual a 2R, ou seja, igual a 12.

Sendo q a razão entre as medidas dos raios das circunferências Cn + 1 e Cn, temos que o raio de C1 mede 4 e seu diâmetro mede 8, o raio de C2 mede 4q e seu diâmetro mede 8q, e assim por diante, de modo que as medidas dos diâmetros das circunferências C1, C2,… formam a seguinte PG infinita de razão q:

(8, 8q, 8q2, …)

A soma de seus infinitos termos deve resultar em 12, ou seja:

começar estilo tamanho matemático 14px atributos de tabela alinhamento de coluna right center left espaçamento de coluna 0px fim dos atributos linha com célula com numerador 8 sobre denominador 1 espaço menos espaço reto q fim da fração espaço fim da célula igual a célula com espaço 12 espaço espaço espaço espaço então fim da célula linha com célula com reto q espaço fim da célula igual a célula com espaço 1 terço fim da célula fim da tabela fim do estilo

c) A área pedida é dada pela diferença entre a área do círculo C, que é igual a π⋅36, e a soma das áreas dos círculos C1, C2, … . Como os raios de C1, C2, … medem, respectivamente, 4, 4q, … , suas áreas são iguais, também respectivamente, a π⋅16, π⋅16q2, … .
Essas áreas formam uma PG infinita de razão q2:

(16π, 16πq2, 16πq4, …)

A soma de seus termos é, portanto:

começar estilo tamanho matemático 14px numerador 16 reto pi sobre denominador 1 espaço menos espaço reto q ao quadrado fim da fração fim do estilo

Como determinado no item anterior, temos começar estilo tamanho matemático 14px reto q espaço igual a espaço 1 terço fim do estilo e, portanto:

começar estilo tamanho matemático 14px numerador 16 reto pi sobre denominador 1 espaço menos espaço reto q ao quadrado fim da fração espaço igual a espaço numerador 16 reto pi sobre denominador 1 espaço menos espaço começar estilo mostrar 1 sobre 9 fim do estilo fim da fração espaço igual a espaço 18 reto pi fim do estilo

Assim, a área pedida é igual a:

36π – 18π = 18π