Considerando A = {1,2,3,4} e B = {1,2,3,4,5,6},

a) quantas funções f: A → A (não necessariamente sobrejetoras) existem?

b) quantas são as funções f: B → B que satisfazem f(f(n)) = n, para todo n ∈ B?

c) escolhendo aleatoriamente uma função f: B → B bijetora, qual é a probabilidade de f ter ao menos um ponto fixo?

Note e adote:
Dizemos que n ∈ B é um ponto fixo de f se f(n) = n.

a) Para que começar estilo tamanho matemático 14px reto f dois pontos espaço reto A espaço seta para a direita espaço reto A fim do estilo exista, é necessário que cada elemento do domínio A esteja associado a um único elemento do contradomínio A. Ou seja, a cada um dos 4 elementos do conjunto A, devemos associar um dos 4 elementos do conjunto A.

Como são 4 elementos no domínio e, para cada um deles, existem 4 possibilidades de associação no contradomínio, o total de funções começar estilo tamanho matemático 14px reto f dois pontos espaço reto A espaço seta para a direita espaço reto A fim do estilo é começar estilo tamanho matemático 14px 4 espaço vezes espaço 4 espaço vezes espaço 4 espaço vezes espaço 4 espaço igual a espaço 256 fim do estilo.

Resposta: 256

b) Se começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço reto y fim do estilo, então começar estilo tamanho matemático 14px reto f parêntese esquerdo reto y parêntese direito espaço igual a espaço reto x fim do estilo. Veja alguns exemplos a seguir.

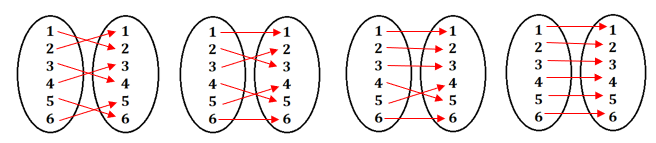
Note que, se houver algum valor x1 do domínio tal que começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 1 subscrito parêntese direito espaço igual a espaço reto x com 1 subscrito fim do estilo, necessariamente haverá um valor x2 do domínio, com começar estilo tamanho matemático 14px reto x com 2 subscrito espaço não igual espaço reto x com 1 subscrito fim do estilo, tal que começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 2 subscrito parêntese direito espaço igual a espaço reto x com 2 subscrito fim do estilo.

Assim, temos 4 casos a considerar:

  • 1º caso: para todo começar estilo tamanho matemático 14px reto x espaço pertence espaço reto B fim do estilo, começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço não igual espaço reto x fim do estilo

Devem ser formados três pares {x, y}, sendo x e y elementos distintos do domínio.

Para formar o primeiro par, devemos escolher dois elementos de B, ou seja:

começar estilo tamanho matemático 14px reto C com 6 vírgula 2 subscrito fim do subscrito espaço igual a numerador 6 fatorial sobre denominador 4 fatorial espaço vezes espaço 2 fatorial fim da fração espaço igual a espaço 15 fim do estilo

Para formar o segundo par, devemos escolher 2 dos 4 elementos restantes:

começar estilo tamanho matemático 14px reto C com 4 vírgula 2 subscrito fim do subscrito espaço igual a espaço numerador 4 fatorial sobre denominador 2 fatorial espaço vezes espaço 2 fatorial fim da fração espaço igual a espaço 6 fim do estilo

Formados os dois primeiros pares, resta apenas uma possibilidade para o terceiro par.

Dessa forma, o total de maneiras de se formar os 3 pares é igual a:

começar estilo tamanho matemático 14px numerador 15 espaço vezes espaço 6 espaço vezes espaço 1 sobre denominador 3 fatorial fim da fração espaço igual a espaço 15 fim do estilo

  • 2º caso: existem apenas dois valores x1 e x2 do domínio, com começar estilo tamanho matemático 14px reto x com 1 subscrito espaço não igual espaço reto x com 2 subscrito fim do estilo, tais que começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 1 subscrito parêntese direito espaço igual a espaço reto x com 1 subscrito fim do estilo e começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 2 subscrito parêntese direito espaço igual a espaço reto x com 2 subscrito fim do estilo

​Devem ser formados dois pares {x, y}, sendo x e y elementos distintos do domínio.

Para formar o primeiro par, devemos escolher dois elementos de B, ou seja:

começar estilo tamanho matemático 14px reto C com 6 vírgula 2 subscrito fim do subscrito espaço igual a espaço numerador 6 fatorial sobre denominador 4 fatorial espaço vezes espaço 2 fatorial fim da fração espaço igual a espaço 15 fim do estilo

Para formar o segundo par, devemos escolher 2 dos 4 elementos restantes:

começar estilo tamanho matemático 14px reto C com 4 vírgula 2 subscrito fim do subscrito espaço igual a espaço numerador 4 fatorial sobre denominador 2 fatorial espaço vezes espaço 2 fatorial fim da fração espaço igual a espaço 6 fim do estilo

Formados os dois primeiros pares, os valores x1 e x2 só podem ser escolhidos de uma maneira.

Dessa forma, o total de maneiras de se formar os 2 pares é igual a:

começar estilo tamanho matemático 14px numerador 15 espaço vezes espaço 6 sobre denominador 2 fatorial fim da fração espaço igual a espaço 45 fim do estilo

  • 3º caso: existem apenas quatro valores x1, x2, x3 e x4 do domínio, distintos dois a dois, tais que começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 1 subscrito parêntese direito espaço igual a espaço reto x com 1 subscrito fim do estilo, começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 2 subscrito parêntese direito espaço igual a espaço reto x com 2 subscrito fim do estilo, começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 3 subscrito parêntese direito espaço igual a espaço reto x com 3 subscrito fim do estilo e começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x com 4 subscrito parêntese direito espaço igual a espaço reto x com 4 subscrito fim do estilo

​Deve ser formado apenas um par {x, y}, sendo x e y elementos distintos do domínio.

Para formá-lo, devemos escolher dois elementos de B, ou seja:

começar estilo tamanho matemático 14px reto C com 6 vírgula 2 subscrito fim do subscrito espaço igual a espaço numerador 6 fatorial sobre denominador 4 fatorial espaço vezes espaço 2 fatorial fim da fração espaço igual a espaço 15 fim do estilo

Formado esse par, os valores x1, x2, x3 e x4 só podem ser escolhidos de uma maneira.

Dessa forma, o total de maneiras de se formar apenas um par é igual a 15.

  • 4º caso: sendo  um elemento qualquer do domínio, temos começar estilo tamanho matemático 14px reto f parêntese esquerdo reto y parêntese direito espaço igual a espaço reto x fim do estilo

Há apenas uma função com essa propriedade.

Dessa forma, o total de funções começar estilo tamanho matemático 14px reto f dois pontos espaço reto B espaço seta para a direita espaço reto B fim do estilo com a característica solicitada é igual a:

começar estilo tamanho matemático 14px 15 espaço mais espaço 45 espaço mais espaço 15 espaço mais espaço 1 espaço igual a espaço 76 fim do estilo

Resposta: 76

c) Inicialmente, vamos contar a quantidade de funções começar estilo tamanho matemático 14px reto f dois pontos espaço reto B espaço seta para a direita espaço reto B fim do estilo que são bijetoras. Para o elemento 1, há 6 possibilidades de associação; para o elemento 2, considerando que começar estilo tamanho matemático 14px reto f parêntese esquerdo 2 parêntese direito espaço não igual espaço reto f parêntese esquerdo 1 parêntese direito fim do estilo, temos 5 possibilidades de associação. Seguindo esse raciocínio para os demais elementos, temos que o total de funções bijetoras começar estilo tamanho matemático 14px reto f dois pontos espaço reto B espaço seta para a direita espaço reto B fim do estilo é igual a:

começar estilo tamanho matemático 14px 6 espaço vezes espaço 5 espaço vezes espaço 4 espaço vezes espaço 3 espaço vezes espaço 2 espaço vezes espaço 1 espaço igual a espaço 720 fim do estilo

Dessas, algumas têm pelo menos um ponto fixo e, as demais, nenhum ponto fixo. Vamos contar as que têm pelo menos um ponto fixo.

  • exatamente 6 pontos fixos: apenas 1 possibilidade.
  • exatamente 5 pontos fixos: não há casos, já que, se f tiver 5 pontos fixos, o 6º ponto também será fixo.
  • exatamente 4 pontos fixos: há começar estilo tamanho matemático 14px reto C com 6 vírgula 4 subscrito fim do subscrito espaço igual a espaço 15 fim do estilo possibilidades de escolha dos 4 pontos fixos e, escolhidos esses pontos, só há uma configuração em que os demais não são fixos. Dessa forma, há um total de 15 casos.
  • exatamente 3 pontos fixos: há começar estilo tamanho matemático 14px reto C com 6 vírgula 3 subscrito fim do subscrito espaço igual a espaço 20 fim do estilo possibilidades de escolha dos 3 pontos fixos e, escolhidos esses pontos, só há 2 configurações em que os demais não são fixos. Dessa forma, há um total de começar estilo tamanho matemático 14px 20 espaço vezes espaço 2 espaço igual a espaço 40 fim do estilo casos.
  • exatamente 2 pontos fixos: há começar estilo tamanho matemático 14px reto C com 6 vírgula 2 subscrito fim do subscrito espaço igual a espaço 15 fim do estilo possibilidades de escolha dos 2 pontos fixos e, escolhidos esses pontos, só há 9 configurações em que os demais não são fixos. Dessa forma, há um total de começar estilo tamanho matemático 14px 15 espaço vezes espaço 9 espaço igual a espaço 135 fim do estilo casos.
  • exatamente 1 ponto fixo: há 6 possibilidades de escolha do ponto fixo e, escolhido esse ponto, só há 44 configurações em que os demais não são fixos. Dessa forma, há um total de começar estilo tamanho matemático 14px 6 espaço vezes espaço 44 espaço igual a espaço 264 fim do estilo casos.

Assim, há um total de começar estilo tamanho matemático 14px 1 espaço mais espaço 15 espaço mais espaço 40 espaço mais espaço 135 espaço mais espaço 264 espaço igual a espaço 455 fim do estilo funções com pelo menos um ponto fixo e, portanto, a probabilidade pedida é igual a:

começar estilo tamanho matemático 14px 455 sobre 720 espaço igual a espaço 91 sobre 144 fim do estilo

Resposta: começar estilo tamanho matemático 14px 91 sobre 144 fim do estilo