Considere a, b, c ∈ ℝ e a função f: ℝ → ℝ dada por f(x) = ax2 + bx + c.
a) Determine os valores de a, b e c para que f(1) = 1, f(0) = 0 e f(−1) = 1.
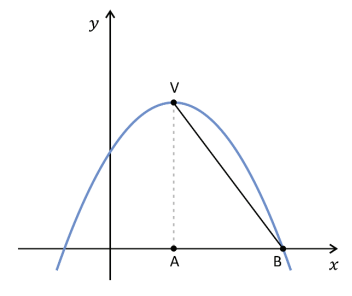
b) Para a = −1 e b = 4, determine o valor de c de modo que a área do triângulo ABV da figura seja igual a 32 u.a., onde V é o vértice da parábola representada por f.
c) Considere g: ℝ → ℝ a função dada por g(t) = cos t. Se a = 3 e c = −8, determine para quais valores de b a equação f(g(t)) = 0 possui ao menos uma solução real.
a) Dado que f(0) = 0, então a·02 + b·0 + c = 0, o que implica c = 0. Além disso, como f(1) = f(–1) = 1, deve-se ter:
Somando as equações, obtém-se 2a = 2 e, portanto, a = 1. Com isso, tem-se b = 0.
b) A abscissa dos pontos A e V é dada por e a abscissa do ponto B é dada por
, ou seja,
. Dessa forma, a base
do triângulo mede
. (I)
A ordenada de V é dada por f(2) = –22 + 4·2 + c, ou seja, 4 + c. Dessa forma, a altura AV do triângulo vale 4 + c. (II)
De (I), (II) e sabendo que a área do triângulo ABV é igual a 32, então deve-se ter:
Com c > –4, note que e, assim:
c) Para que a equação dada tenha pelo menos uma solução real, como –1 ≤ g(t) ≤ 1, é necessário e suficiente que as raízes da equação f(x) = 0 sejam reais e que pelo menos uma delas pertença ao intervalo [–1,1].
Para que as raízes sejam reais, o discriminante dessa equação deve ser não negativo, o que ocorre se, e somente se, , ou seja, se
. Como b2 + 96 é a soma de dois números reais positivos, então essa expressão é um número real não negativo para qualquer valor real de . Assim, basta que pelo menos uma das raízes pertença ao intervalo [–1,1].
Denotando por x1 e x2 essas raízes, note que e, assim, é impossível que ambas estejam em [–1,1]. Logo, é necessário que alguma dessas raízes pertença a esse intervalo.
Para que isso ocorra, o gráfico da função deve intersectar o eixo das abscissas em algum número em [–1,1], o que ocorre se, e somente se, f(1) ≥ 0 e f(–1) < 0 ou se f(1) < 0 e f(–1) ≥ 0.
De qualquer forma, pode-se escrever f(–1)·f(1) ≤ 0:
Resolvendo essa inequação, obtém-se b ≤ –5 ou b ≥ 5.