Márcia está decorando sua casa para o Natal e pretende cobrir uma pilastra com um papel de parede de temas natalinos e depois enrolar uma fita de lâmpadas de led na pilastra coberta, dando uma única volta, de modo que o ponto em que a fita começa a ser enrolada esteja exatamente embaixo do ponto onde ela termina, como ilustrado na figura a seguir.
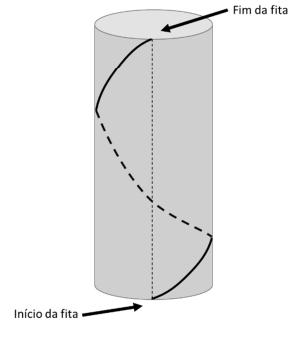
A pilastra tem o formato de um cilindro circular reto com 3 m de altura; a medida do perímetro da circunferência da base é 1 m, e sua lateral será coberta completamente com papel de parede colado sem sobreposição.
a) Sabendo que o metro quadrado do papel de parede custa R$ 20,00, determine quanto Márcia terá que gastar em papel de parede para cobrir a pilastra como ela quer.
b) Qual é o menor comprimento que a fita de led precisa ter para ser possível esta instalação?
a) A superfície lateral do cilindro é um retângulo de base medindo 1 m e altura igual a 3 m, de modo que sua área é 3 m2. Como cada metro quadrado do papel de parede custa R$ 20,00, o gasto com o papel é de R$ 60,00.
b) Planificando-se a superfície lateral do cilindro, temos que a fita de led tem seu menor comprimento quando coincide com a diagonal do retângulo, como exibido na figura a seguir, cotada em metros.
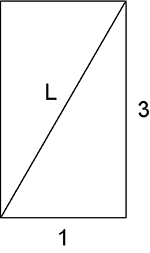
Pelo teorema de Pitágoras, o comprimento L, em metro, da fita é dado por: