Sejam a b, ∈ ℝ com a ≠ 0 e f(x) = ax2 + bx − 3 uma função polinomial.

a) Determine a,b de forma que o vértice da parábola y = f(x) seja (–1, –4).

b) Para a = –2, determine todos os valores de b de forma que a parábola e a reta y = 2x − 1 se interceptem em dois pontos distintos.

a) Como o ponto (–1; –4) pertence ao gráfico de y = f(x), temos que:

começar estilo tamanho matemático 14px f parêntese esquerdo menos 1 parêntese direito espaço igual a espaço menos 4 espaço espaço espaço espaço espaço então espaço espaço espaço espaço espaço a vezes parêntese esquerdo menos 1 parêntese direito ao quadrado espaço mais espaço b vezes parêntese esquerdo menos 1 parêntese direito espaço menos espaço 3 espaço igual a espaço menos 4 então espaço espaço espaço espaço a espaço menos espaço b espaço igual a espaço menos 1 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço parêntese esquerdo 1 parêntese direito fim do estilo

Além disso, (–1; –4) é o vértice. Assim:

começar estilo tamanho matemático 14px menos numerador reto b sobre denominador 2 reto a fim da fração espaço igual a espaço menos 1 espaço espaço espaço espaço espaço então espaço espaço espaço espaço espaço reto b espaço igual a espaço 2 reto a fim do estilo

Substituindo essa relação em (1), vem:

a – 2a = –1     ∴      a = 1    e    b = 2

b) As abscissas dos pontos em que a parábola de equação f(x) = –2x2 + bx – 3 e a reta de equação y = 2x – 1 se interceptam (caso existam) são dadas pelas raízes reais da equação:

–2x2 + bx – 3 = 2x – 1

–2x2 + bx – 3 – 2x + 1 = 0

–2x2 + (b – 2)x – 2 = 0

Para que a parábola e a reta se interceptem em dois pontos distintos, essa equação deve admitir duas raízes reais e distintas. Assim devemos obter os valores de b, para os quais o discriminante (Δ) da equação é positivo.

Δ = (b – 2)2 – 4∙(–2)∙(–2) > 0

b2 – 4b – 12 > 0

Analisando o sinal vem:

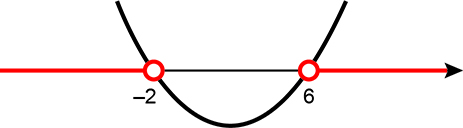
Logo b < –2 ou b > 6.