A World Series é a decisão do campeonato norte-americano de beisebol. Os dois times que chegam a essa fase jogam, entre si, até sete partidas. O primeiro desses times que completar quatro vitórias é declarado campeão.
Considere que, em todas as partidas, a probabilidade de qualquer um dos dois times vencer é sempre
Qual é a probabilidade de o time campeão ser aquele que venceu a primeira partida da World Series?
Sejam A e B os times que chegaram à World Series e considere que o time A venceu a primeira partida. A equipe A pode ser campeã nos seguintes cenários:
a) ganhando os jogos 2, 3 e 4:
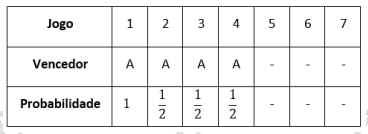
Esse cenário acontece com probabilidade:
b) perdendo um e ganhando dois dos jogos de 2 a 4, e ganhando o jogo 5. Um exemplo em que isso acontece é:
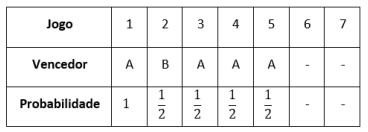
Considerando que os resultados dos jogos 2 a 4 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BAA, ou . Assim, esse cenário acontece com probabilidade:
c) perdendo dois e ganhando dois dos jogos de 2 a 5, e ganhando o jogo 6. Um exemplo em que isso acontece é:
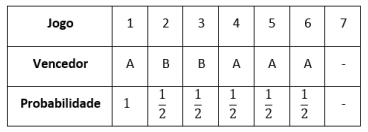
Considerando que os resultados dos jogos 2 a 5 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BBAA, ou . Assim, esse cenário acontece com probabilidade:
d) perdendo três e ganhando dois dos jogos de 2 a 6, e ganhando o jogo 7. Um exemplo em que isso acontece é:

Considerando que os resultados dos jogos 2 a 6 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BBBAA, ou . Assim, esse cenário acontece com probabilidade:
Portanto, o time que venceu a primeira partida é campeão com probabilidade: