De um paralelepípedo reto-retângulo de dimensões 20 cm por cm por
cm serão retirados dois cubos, cujos lados medem x cm. Esses cubos têm três arestas contidas em três arestas do paralelepípedo e uma das faces contida em uma mesma face quadrada do paralelepípedo.
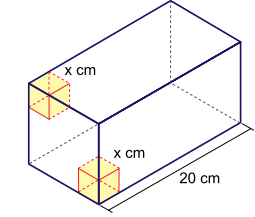
Ao adotar o valor máximo para x, o volume do prisma remanescente, após a retirada dos cubos, será igual a:
Como ambos os cubos têm uma das faces contida em uma mesma face do paralelepípedo, o maior valor possível para x é a metade da medida de comprimento , ou seja,
.
Nesse caso, o volume do sólido (*) restante é:
(*) Ao contrário do que o enunciado diz, o sólido restante após a retirada dos cubos não é um prisma.