Nos instrumentos musicais de corda, as cordas apresentam diferentes espessuras e diferentes densidades lineares de massa, para que aquelas que emitem sons mais graves não precisem ser muito longas, o que inviabilizaria a construção do instrumento.
Detalhes das cordas de um violoncelo

Para ilustrar o fato de que cordas que emitem sons mais graves precisariam ser muito longas, considere duas cordas, 1 e 2, ambas com extremidades fixas, que apresentem espessuras iguais, mesma densidade linear de massa e que estejam submetidas à mesma força de tração.
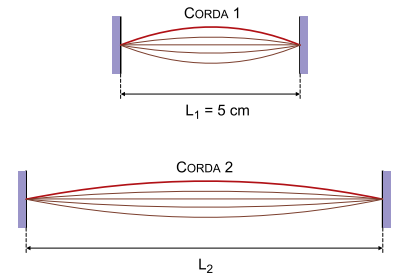
Quando essas cordas vibram em seus modos fundamentais, a frequência da onda sonora emitida pela corda 1 é 150 vezes maior do que a frequência da onda sonora emitida pela corda 2. Sabendo que a corda 1 mede L1 = 5 cm, o comprimento L2 da corda 2 deve ser de
Uma vez que as cordas apresentam as mesmas características físicas (mesma densidade linear e submetidas à mesma intensidade da força de tração), de acordo com a Lei de Taylor, as velocidades das ondas nas cordas 1 e 2 apresentam o mesmo valor (v1 = v2).
A partir do enunciado temos: f1 = 150·f2. Além disso, devemos lembrar que a distância entre dois nós consecutivos de uma onda estacionária corresponde à metade do comprimento de onda. Algebricamente:
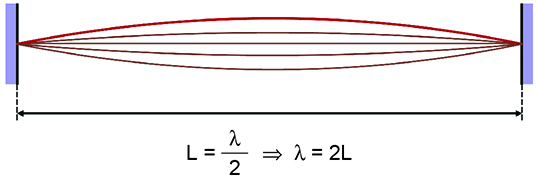
Utilizando a equação fundamental da ondulatória, temos:
Combinando as informações, segue:
Substituindo L1 = 5 cm e f1 = 150·f2:
Portanto:
L2 = 750 cm = 7,5 m.