Em um dia de treinamento, dois amigos, Alberto e Bernardo, decidem dar voltas consecutivas em um circuito de 1000 m de comprimento, partindo simultaneamente de um mesmo ponto, porém movendo-se em sentidos opostos. Alberto caminha no sentido horário e Bernardo corre no sentido anti- -horário com velocidade três vezes maior do que a de Alberto. Os dois mantêm suas velocidades escalares constantes.
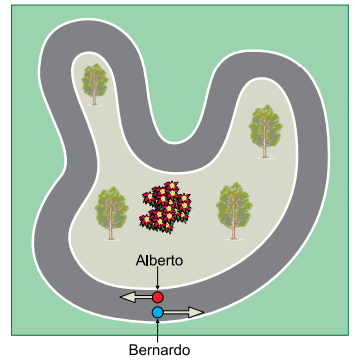
Após o início desse treinamento, no instante em que ocorrer o terceiro encontro entre os dois, Alberto e Bernardo terão percorrido, respectivamente,
Como o módulo da velocidade do Bernardo é igual ao triplo do módulo da velocidade do Alberto, quando Alberto percorrer uma distância X, Bernardo terá percorrido uma distância 3X. Além disso, quando ocorrer o primeiro encontro, a soma das distâncias percorridas pelos amigos será igual ao comprimento da pista, ou seja, 1 000 m. Assim,
X + 3X = 1 000 → X = 250 m.
Dessa forma, até o primeiro encontro, Alberto terá percorrido X = 250 m e Bernardo, 3X = 750 m. A partir desse instante, até o encontro seguinte, os dois amigos percorrerão essas mesmas distâncias. Portanto, até o terceiro encontro, eles terão percorrido o triplo dessas distâncias, ou seja, Alberto terá percorrido 3·250 m = 750 m, e Bernardo, 3·750 m = 2 250 m.