Em um sorteio com cartelas numeradas de 0001 a 2000, João decidiu comprar todas as cartelas em que a numeração exibisse os números 2 e 5, e nenhuma a mais. Por exemplo, João comprou as cartelas 1205 e 0025, mas não comprou as cartelas 0514 e 2000.
Considere as afirmações:
I) João comprou 108 cartelas.
II) Se ao invés das cartelas com 2 e 5, João tivesse comprado as cartelas com 1 e 5, ele teria comprado menos cartelas.
III) João comprou 18 cartelas que possuem o número 3.
Assinale a alternativa correta:
Vamos avaliar cada uma das afirmações.
Afirmação I: As possibilidades para que tenham 2 e 5 na cartela são:
Apenas um 2 e um 5.
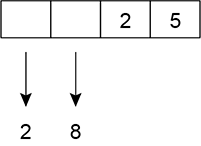
Note também que qualquer permutação entre os algarismos das centenas, dezenas e unidades.
Assim, o total de possibilidades é
Dois 2 e um 5.
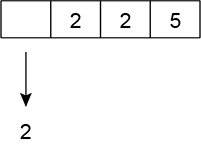
Note também que qualquer permutação entre os algarismos das centenas, dezenas e unidades.
Assim, o total de possibilidades é
Um 2 e dois 5.
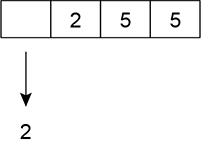
Note também que qualquer permutação entre os algarismos das centenas, dezenas e unidades.
Assim, o total de possibilidades é
Desse modo o total de cartelas é .
Logo a afirmação I é verdadeira.
Afirmação II: As possibilidades para que tenham 1 e 5 certamente aumentam com relação à anterior, pois agora podem-se considerar números com o algarismo dos milhares começados em 1, o que não era possível antes.
Logo a afirmação II é falsa.
Afirmação III: As possibilidades para que tenham 2, 5 e 3 na cartela são:
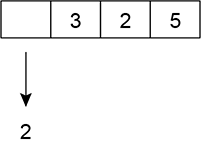
Note também que qualquer permutação entre os algarismos das centenas, dezenas e unidades.
Assim, o total de possibilidades é
Logo a afirmação III é falsa.