A figura seguinte mostra um triângulo retângulo ABC. O ponto M é o ponto médio do lado AB, que é a hipotenusa.
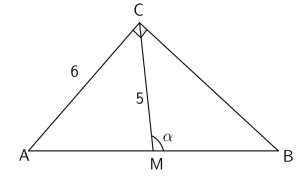
O valor de sen α é
Lembrando que a medida da mediana relativa à hipotenusa mede metade da hipotenusa, tem-se que e, consequentemente,
.
Além disso, aplicando o teorema de Pitágoras no triângulo ACB, tem-se que .
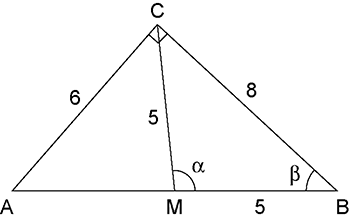
Agora, aplicando o teorema dos senos no triângulo CMB, vem: