A figura A apresenta um esquema simplificado de um refratômetro, destinado a determinar o índice de refração n1 de um líquido. Nele, o líquido é iluminado por raios que o atravessam, atingindo, na parte superior, um vidro de índice de refração conhecido n2 = 1,8. Quando o θ1 = 90 , temos o máximo valor para o ângulo de refração θ2, que, nesse caso, é chamado de ângulo crítico, θC (ver figura B).
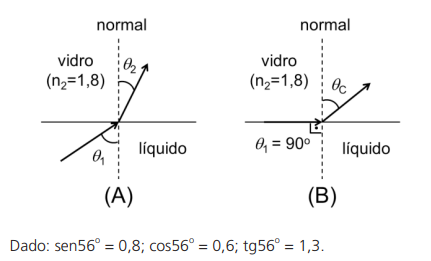
Se o ângulo crítico medido foi θC = 56o, pode-se dizer que o índice de refração do líquido em questão é
O seno do ângulo limite (ângulo crítico: θC = 56o) é dado por:
Como o ângulo crítico é formado sempre no meio mais refringente, conclui-se que o vidro é o meio mais refringente (nvidro = nmaior), enquanto o líquido é o meio menos refringente (nlíquido = nmenor).
Assim, na expressão acima, temos:
Note que, se o índice de refração do líquido for maior que 1,44, o valor de sen θc também aumenta, podendo, matematicamente chegar a um valor máximo igual a 1.
Quando o seno de um ângulo aumenta, o valor do ângulo também aumenta (lembrando que, para as situações de óptica, valem apenas ângulos que pertençam ao primeiro quadrante trigonométrico).
Concluindo: se trocarmos o líquido por outro de índice de refração maior, o ângulo crítico será maior que 56o.