Em um local em que a aceleração gravitacional é igual a 10 m/s2, um projétil de massa 8,0 g foi disparado obliquamente de tal forma que as componentes horizontal e vertical da sua velocidade inicial eram, respectivamente, 300 m/s e 120 m/s.
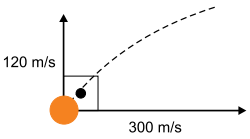
a) Na ausência de resistência do ar, esse projétil descreveria uma trajetória parabólica resultado da composição de um movimento uniforme, na direção horizontal, e de um movimento uniformemente variado, na direção vertical. Nesse caso, calcule, em metros, as distâncias horizontal e vertical percorridas por esse projétil, após 2,0 segundos do instante do lançamento.
b) Considere que, devido à resistência do ar, esse projétil atingiu o ponto mais alto da sua trajetória com velocidade horizontal de 100 m/s. Sabendo que a intensidade da força de resistência do ar que atuava sobre o projétil nesse instante, era dada, em newtons, por FA = 6,0 × 10–6 ⋅ v2, em que v é a intensidade da velocidade do projétil em m/s, calcule, em newtons, a intensidade da força resultante que atuou sobre esse projétil no ponto mais alto da sua trajetória.
a) A figura a seguir apresenta a situação descrita no enunciado com eixos x e y para estudar o problema proposto:
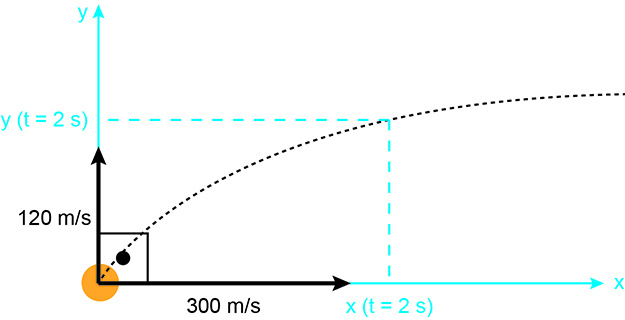
As equações que relacionam as posições nos eixos x e y podem assim ser representadas:
Em x (Movimento Uniforme – MU):
Em y (Movimento Uniformemente Variado – MUV):
Calculando as posições x e y para t = 2 s, temos:
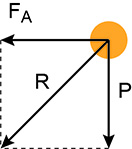
b) As forças que atuam no projétil são a peso (P) e a resistência do ar (FA). A força peso tem direção vertical e sentido para baixo, enquanto a resistência do ar tem sentido contrário à da velocidade.
No ponto de altura máxima, a componente vertical (vy) é zero. Portanto, a velocidade que o corpo desenvolve coincide com sua componente horizontal (vx), assim:
Aplicando a expressão fornecida no enunciado, obtemos a intensidade da força de resistência do ar (FA):
A intensidade da força peso será dada por:
Portanto, podemos encontrar a Resultante das Forças de acordo com a imagem a seguir: