Anglo Resolve

Questão 90

Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal, é representado pela matriz coluna , assim como a matriz coluna representa, no plano cartesiano ortogonal, o ponto P de coordenadas (x, y).

Sendo assim, o resultado da multiplicação matricial é uma matriz coluna que, no plano cartesiano ortogonal, necessariamente representa um ponto que é

a
uma rotação de P em 180º no sentido horário, e com centro em (0, 0).
b
uma rotação de P em 90º no sentido anti-horário, e com centro em (0, 0).
c
simétrico de P em relação ao eixo horizontal x.
d
simétrico de P em relação ao eixo vertical y.
e
uma rotação de P em 90º no sentido horário, e com centro em (0, 0).

Resolução

Efetuando o produto das matrizes, temos:

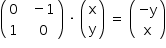
Note-se então que essa matriz transforma o ponto P(x, y) no ponto Q(–y, x). Sem perda de generalidade, podemos supor que P pertence ao 1º quadrante. Logo, temos:

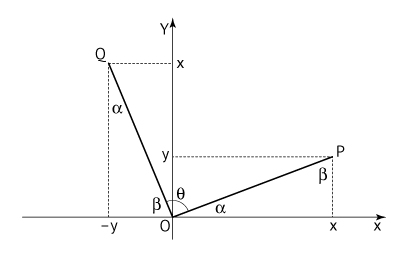
Os triângulos retângulos de hipotenusas OP e OQ são congruentes; assim, temos, da figura, que α + β + θ = 180°. Como α + β = 90°, então devemos ter θ = 90°.
Portanto, o ponto Q é uma rotação de 90^o do ponto P, no sentido anti-horário, com centro (0, 0).