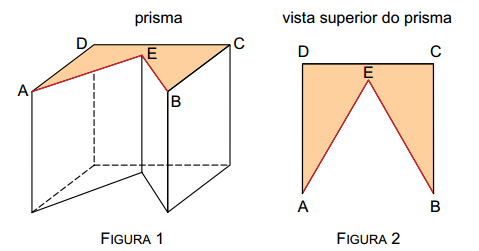
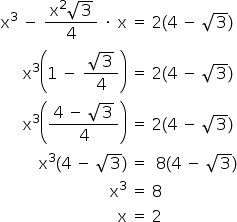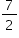Um cubo com aresta de medida igual a x centímetros foi seccionado, dando origem ao prisma indicado na figura 1. A figura 2 indica a vista superior desse prisma, sendo que AEB é um triângulo equilátero.
Sabendo-se que o volume do prisma da figura 1 é igual a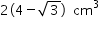 
, x é igual a
- a
2
- b
- c
3
- d
- e
O volume do prisma indicado pode ser dado pela diferença entre os volumes do cubo e do prisma cuja base é o triângulo equilátero AEB, cujo lado também mede x cm (vide figura 2). Assim:
