Uma mesa de passar roupa possui pernas articuladas 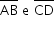 , conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares
, conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares 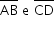 . Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo A
. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo A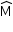 C é 60º.
C é 60º.
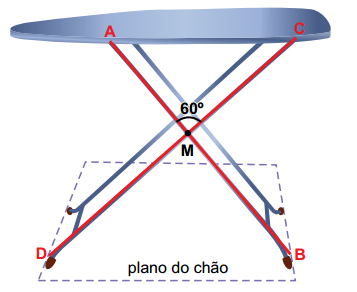
Considerando-se desprezíveis as medidas dos pés e da espessura do tampo e adotando 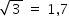 , a altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre
, a altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre
Do enunciado, temos que os triângulos AMC e DMB são equiláteros, como mostra a figura abaixo.
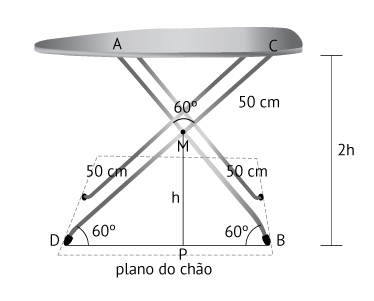
Dessa figura, temos, no triângulo retângulo DMP:
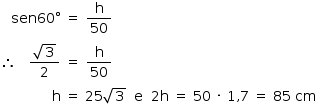
Logo, a altura pedida está entre 84 cm e 87 cm.