Um experimento foi feito com a finalidade de determinar a frequência de vibração de um diapasão. Um tubo cilíndrico aberto em suas duas extremidades foi parcialmente imerso em um recipiente com água e o diapasão vibrando foi colocado próximo ao topo desse tubo, conforme a figura 1. O comprimento L da coluna de ar dentro do tubo foi ajustado movendo-o verticalmente. Verificou-se que o menor valor de L, para o qual as ondas sonoras geradas pelo diapasão são reforçadas por ressonância dentro do tubo, foi de 10 cm, conforme a figura 2.
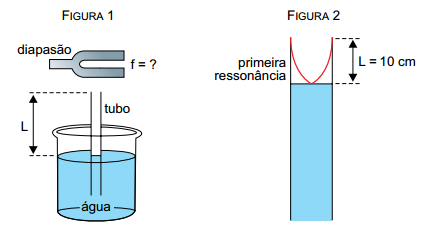
Considerando a velocidade de propagação do som no ar igual a 340 m/s, é correto afirmar que a frequência de vibração do diapasão, em Hz, é igual a
A partir da figura 2, que representa a primeira ressonância, pode-se calcular sua frequência:
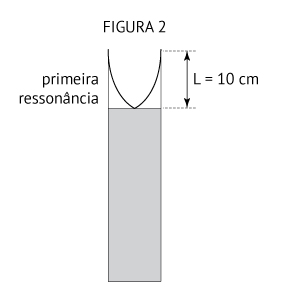
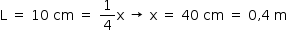
Utilizando a equação fundamental da ondulatória:
v = λ f → 340 = 0,4f – f = 850 Hz.
Como há ressonância entre o diapasão e o tubo,
ftubo = fdiapasão = 850 Hz