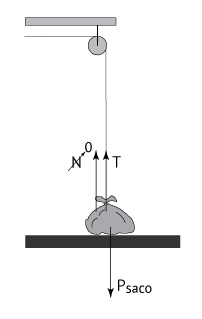
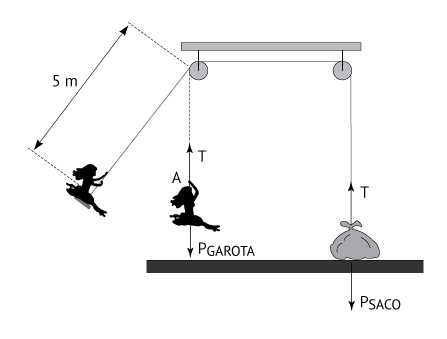
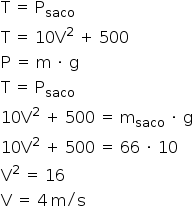Uma garota de 50 kg está brincando em um balanço constituído de um assento e de uma corda ideal que tem uma de suas extremidades presa nesse assento e a outra, em um saco de areia de 66 kg que está apoiado, em repouso, sobre o piso horizontal. A corda passa por duas roldanas ideais fixas no teto e, enquanto oscila, a garota percorre uma trajetória circular contida em um plano vertical de modo que, ao passar pelo ponto A, a corda fica instantaneamente vertical.
Desprezando a resistência do ar e a massa do assento, considerando g = 10 m/s2 e as informações contidas na figura, a maior velocidade, em m/s, com a qual a garota pode passar pelo ponto A sem que o saco de areia perca contato com o solo é igual a
Observe a figura a seguir:
Na situação limite para que o saco de areia não perca o contato com o chão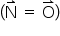 
, tem-se que a força tração do fio é igual ao peso do saco de areira 
.
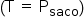Como a garota encontra-se em movimento, pode-se calcular o valor da força tração (T) a partir da resultante centrípeta no ponto A, cuja trajetória circular tem raio R = 5,0m:
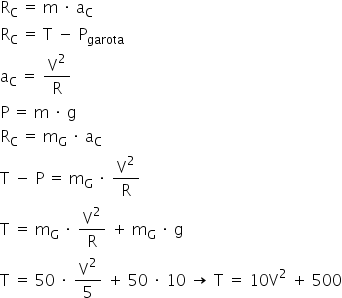
Portanto, na situação limite:
