Sabe-se atualmente que os prótons e nêutrons não são partículas elementares, mas sim partículas formadas por três quarks. Uma das propriedades importantes do quark é o sabor, que pode assumir seis tipos diferentes: top, bottom, charm, strange, up e down. Apenas os quarks up e down estão presentes nos prótons e nos nêutrons. Os quarks possuem carga elétrica fracionária. Por exemplo, o quark up tem carga elétrica igual a qup = + 2 / 3 q e o quark down qdown = - 1/ 3 e, onde e é o módulo da carga elementar do elétron.
a) Quais são os três quarks que formam os prótons e os nêutrons?
b) Calcule o módulo da força de atração eletrostática entre um quark up e um quark down separados por uma distância d=0,2 x 10-15 m. Caso necessário, use K = 9 x 109 Nm2/C2 e e = 1,6 x 10-19 C.
a) O próton tem carga qP = +e, então a única possibilidade de combinação dos três quarks é: up, up e down.
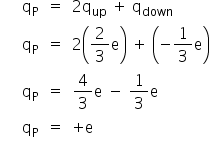
O nêutron tem carga qN = 0, então a única possibilidade de combinação dos três quarks é: up, down e down.
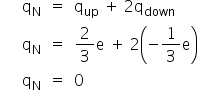
b) Aplicando a lei de Coulomb:
